Günümüzde hemen hemen her alanda kullanılan Analitik Geometri, yaşamımızın değişmez bir parçası oldu. Tarımdan tutundan da inşaat sektörüne kadar hemen hemen her iş alanında karşımıza çıkan Analitik Geometri, hayatımızı kolaylaştırıyor. Bugünkü yazımızda sizlere Analitik Geometri formülleri hakkında bilgi vereceğiz.
Teknoloji her ne kadar sürekli gelişip ilerlese de, eskiden bugüne kadar Analitik Geometri insan hayatını kolaylaştırmıştır. İnsanlar hemen hemen her finansal alanda bu formüllere başvurmuştur. Ayrıca lise döneminde de öğrencilerin karşısına sıklıkla çıkan bu formüller, sınavlarda kilit noktayı oynamaktadır.
Matematik ile ilgili olun ya da olmayın, hayatınızda en az bir kere Analitik Geometriyi kullanmışsınızdır. Sizlere önereceğimiz formüller ile beraber hem sınav hayatınızda kolaylıkla bu sorunların üstesinden gelebilir, hem de gündelik hayatta kullanabilirsiniz. Dilersiniz şimdi bu formülleri inceleyelim.
Doğrunun Eğimi
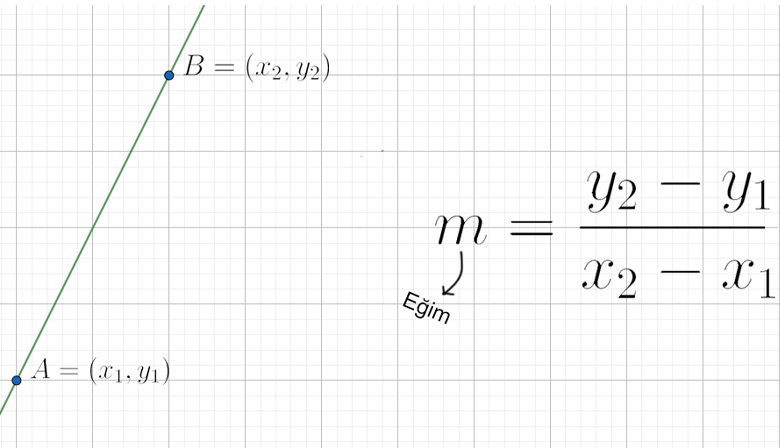
Bir doğrunun eğimi, doğrunun yataylığını ve aynı zamanda değer değişimini ifade eder.
Doğru ile Nokta Arasındaki Dik Uzaklık
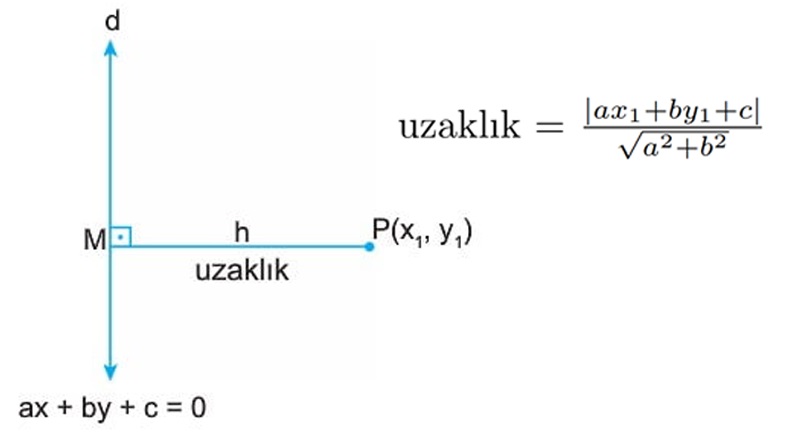
Matematikte, uzaklık birden fazla şekilde tanımlanabilir. Bu karmaşayı engellemek için dik uzaklık kullanılır. İki nokta arasındaki uzaklıktan türetilebilen bu formül yukarıdaki gibi ifade edilir.
Eksenleri Kestiği Noktaları Belli Olan Doğrunun Denklemi
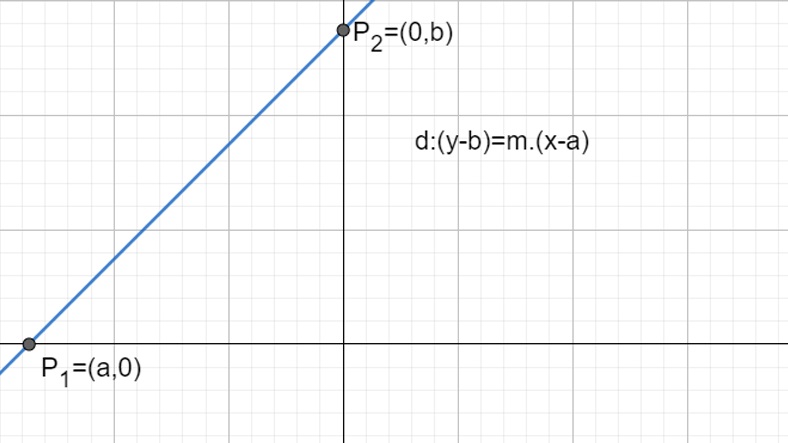
Bir doğruyu analitik düzlemde ifade etmek için bazı verilere ihtiyacımız var. Eğer eksenlerin kestiği noktaları bilirsek doğruyu yukarıdaki gibi ifade edebiliriz.
Doğru Demeti
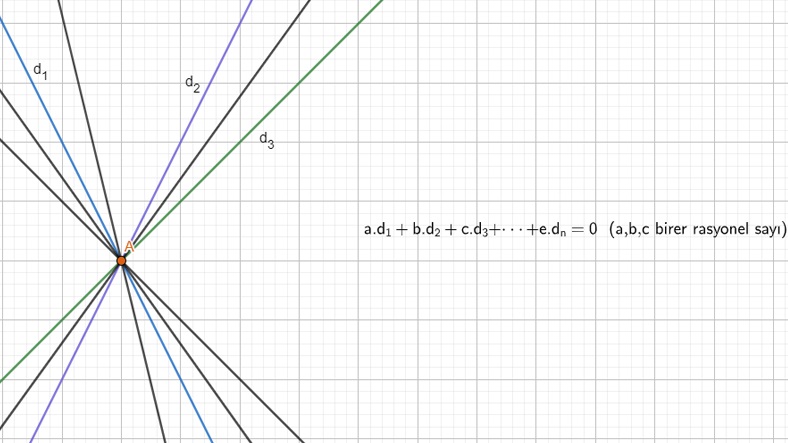
Bir noktada kesişen n tane doğrunun formülünü bilirsek, o noktadan geçen sonsuz tane doğru bulmamız mümkün olur.
Kesişen İki Doğru Arasındaki Açı
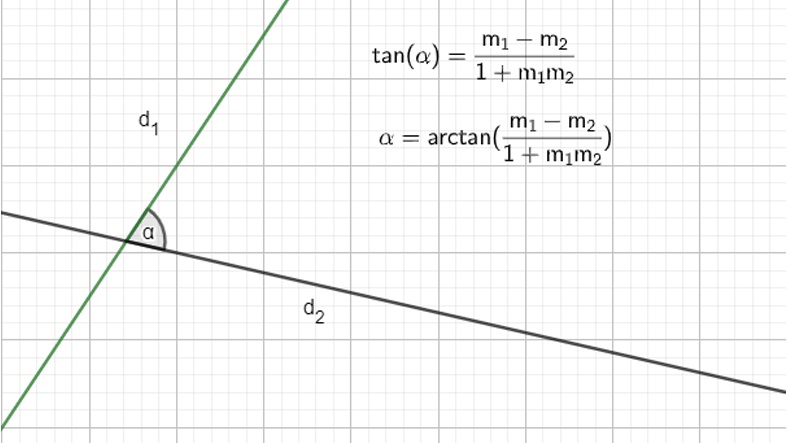
Birçok geometrik şekli yorumlamamız sağlayan şeylerden biri de açılardır. Burada da pek çok geometrik şeklin temelini görüyoruz.
Analitik Bir Yapıyı Döndürme ve Öteleme
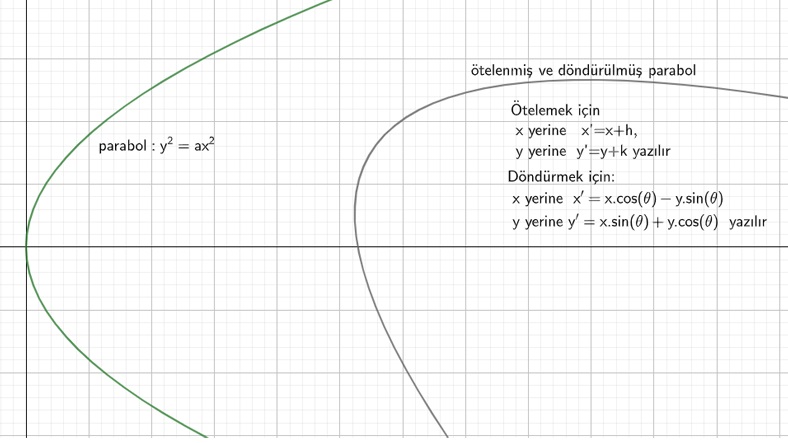
Analitik bir düzlemde ifade edebildiğimiz herhangi bir şeyi istediğimiz yere öteleyebilir ve istediğimiz dereceyle döndürebiliriz.
Dörtgenin Alanı
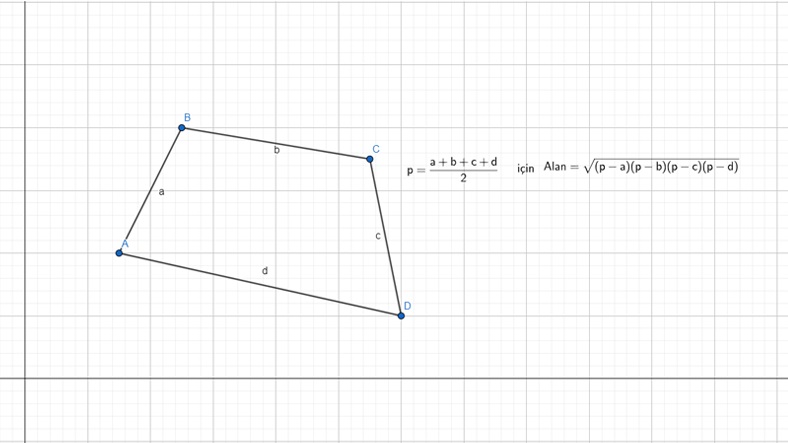
Özellikle, arazi ölçümleri ve tarımsal alanların tasarlanmasında sık sık alan hesaplarından faydalanılır. Geçmiş uygarlıklarda verimli ekin yapmak için kullanıldığı da görülmüştür.
Üçgenin Alanı
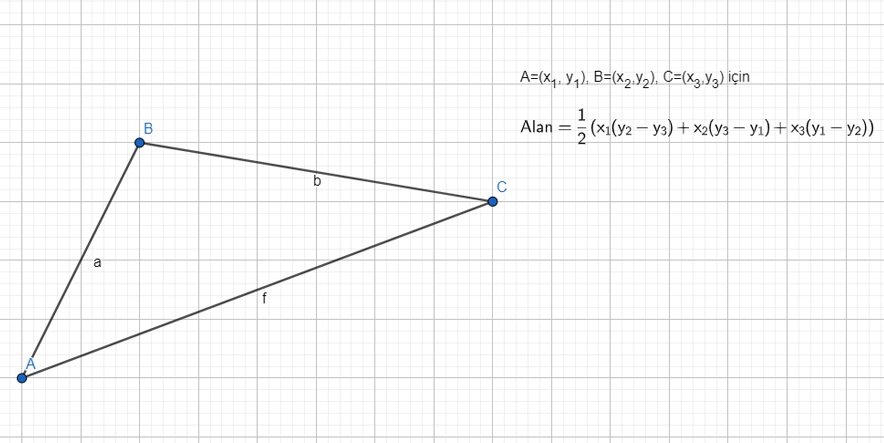
Matematikte bazı operatörleri farklı amaçlarla da kullanabiliriz, üç köşesi verilen bir üçgenin alanını da multi-lineer bir fonksiyon olan determinant ile yukarıdaki gibi hesaplayabiliriz.
Homojen Düzlemsel Bir Cismin Ağırlık Merkezi
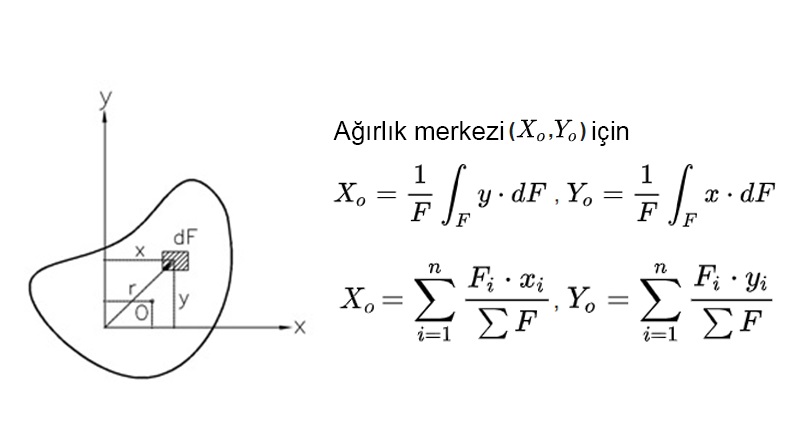
Herhangi n sayıda parçadan oluşan homojen düzlemsel bir cismin, seçilen bir eksen takımına göre ağırlık merkezi yeri olan (X, Y) noktası yukarıdaki bağıntılar ile hesaplanabilir.
Genel Konik Denklemi
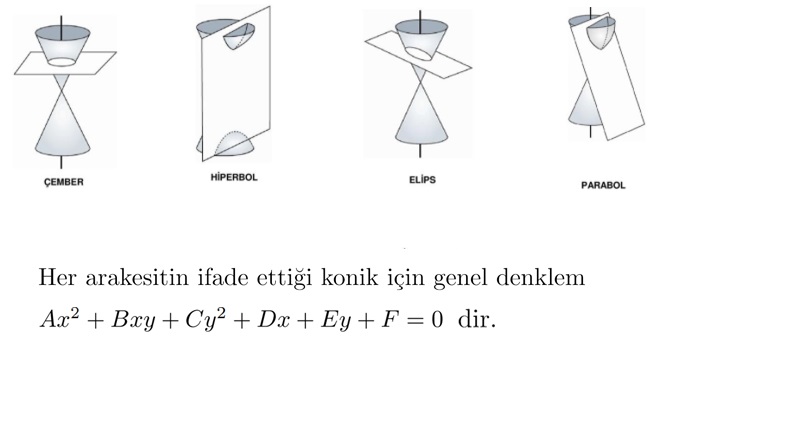
Parabol, çember, elips ve hiperbol gibi konik yapılar aslında bir koninin kesitleridir. Yukarıdaki formül ile bütün bu konik yapıları ifade edebiliriz.
En İyi Çeviri Siteleri, Neredeyse Hatasız Çeviri Yapan Siteler!